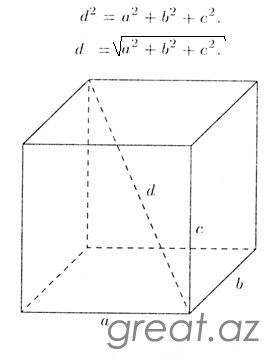
Прямоугольный параллелепипед - это один из видов многогранников, который состоит из шести граней, каждая из которых представляется прямоугольником. Диагональю называется отрезок, соединяющий противоположные вершины параллелограмма. Длину диагонали можно найти двумя способами.
Способ 1.
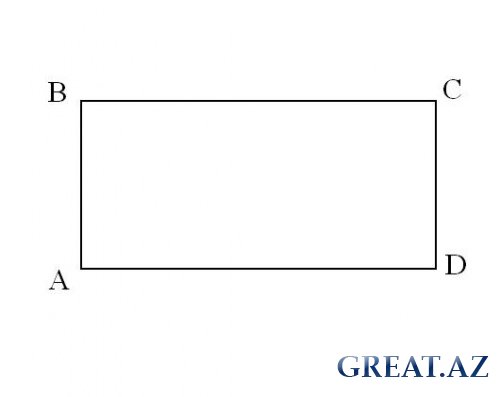
Имеется прямоугольный параллелепипед со сторонами a, b, c и диагональю d. В соответствии с одним из свойств параллелограмма, квадрат диагонали равен сумме квадратов трех его сторон. Исходя из этого следует, что длина диагонали рассчитывается с помощью извлечения квадрата из данной суммы (рис.1).
Способ 2.
Предположим, что прямоугольный параллелепипед представлен в виде куба. А куб - это прямоугольный параллелепипед, каждая грань которого является квадратом. Таким образом, все его стороны равны. И формула для расчеты длины диагонали прямоугольного параллелепипеда будет выглядеть так:
d = a*√3
Способ 1.
Имеется прямоугольный параллелепипед со сторонами a, b, c и диагональю d. В соответствии с одним из свойств параллелограмма, квадрат диагонали равен сумме квадратов трех его сторон. Исходя из этого следует, что длина диагонали рассчитывается с помощью извлечения квадрата из данной суммы (рис.1).

Способ 2.
Предположим, что прямоугольный параллелепипед представлен в виде куба. А куб - это прямоугольный параллелепипед, каждая грань которого является квадратом. Таким образом, все его стороны равны. И формула для расчеты длины диагонали прямоугольного параллелепипеда будет выглядеть так:
d = a*√3