Поиск площади треугольника - одна из самых распространенных задач школьной планиметрии. Знания трех сторон треугольника достаточно для определения площади любого треугольника. В частных случаях равнобедренного и равностороннего треугольников достаточно знать длины двух и одной стороны соответственно.

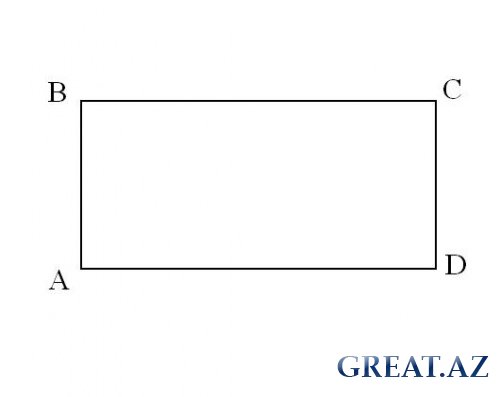
Пусть задана треугольник ABC со сторонами AB = c, AC = b, BC = a. Площадь такого треугольника можно найти по формуле Герона.
Периметр треугольника P - это сумма длин его трех сторон: P = a+b+c. Обозначим его полупериметр за p. Он будет равен p = (a+b+c)/2.
Формула Герона для площади треугольника выглядит следующим образом: S = sqrt(p(p-a)(p-b)(p-c)). Если расписать полупериметр p, то получится: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c)/2)) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4.
Можно вывести формулу для площади треугольника и из других соображений, например, применив теорему косинусов.
По теореме косинусов AC^2 = (AB^2)+(BC^2)-2*AB*BC*cos(ABC). Используя введенные обозначения, эти выражения можно также записать в виде: b^2 = (a^2)+(c^2)-2a*c*cos(ABC). Отсюда, cos(ABC) = ((a^2)+(c^2)-(b^2))/(2*a*c)
Площадь треугольника находится также по формуле S = a*c*sin(ABC)/2 через две стороны и угол между ними. Синус угла ABC можно выразить через его косинус с помощью основного тригонометрического тождества: sin(ABC) = sqrt(1-((cos(ABC))^2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.

Пусть задана треугольник ABC со сторонами AB = c, AC = b, BC = a. Площадь такого треугольника можно найти по формуле Герона.
Периметр треугольника P - это сумма длин его трех сторон: P = a+b+c. Обозначим его полупериметр за p. Он будет равен p = (a+b+c)/2.
Формула Герона для площади треугольника выглядит следующим образом: S = sqrt(p(p-a)(p-b)(p-c)). Если расписать полупериметр p, то получится: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c)/2)) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4.
Можно вывести формулу для площади треугольника и из других соображений, например, применив теорему косинусов.
По теореме косинусов AC^2 = (AB^2)+(BC^2)-2*AB*BC*cos(ABC). Используя введенные обозначения, эти выражения можно также записать в виде: b^2 = (a^2)+(c^2)-2a*c*cos(ABC). Отсюда, cos(ABC) = ((a^2)+(c^2)-(b^2))/(2*a*c)
Площадь треугольника находится также по формуле S = a*c*sin(ABC)/2 через две стороны и угол между ними. Синус угла ABC можно выразить через его косинус с помощью основного тригонометрического тождества: sin(ABC) = sqrt(1-((cos(ABC))^2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.