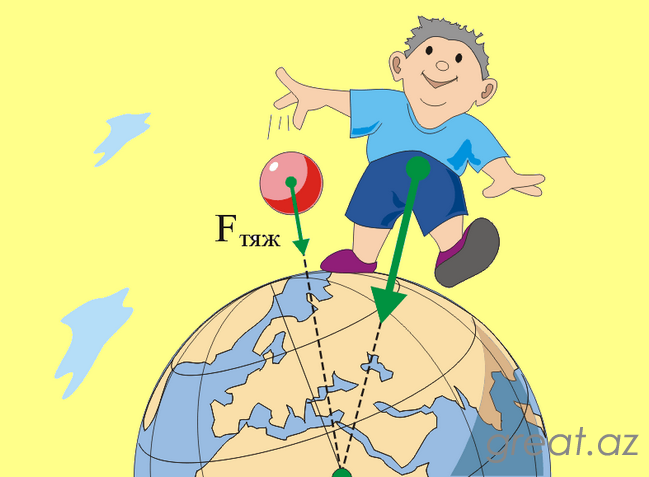
Ньютон называл массой количество материи. Сейчас ее определяют как меру инертности тел: чем тяжелее предмет, тем труднее придать ему ускорение. Чтобы найти инертную массу тела, сравнивают давление, оказываемое им на поверхность опоры, с эталоном, вводят шкалу измерения. Для вычисления массы небесных тел используют гравиметрический метод.
Все тела, обладающие массой, возбуждают в окружающем пространстве гравитационные поля, подобно тому, как электрически заряженные частицы образуют вокруг себя электростатическое поле. Можно предположить, что тела несут в себе гравитационный заряд, аналогичный электрическому, или, по-другому, обладают гравитационной массой. С высокой точностью было установлено, что инертная и гравитационная массы совпадают.
Пусть имеется два точечных тела массами m1 и m2. Они удалены друг от друга на расстояние r. Тогда сила гравитационного притяжения между ними равна: F=C·m1·m2/r², где С – коэффициент, который зависит лишь от выбранных единиц измерения.
Если на поверхности Земли имеется небольшое тело, его размерами и массой можно пренебречь, т.к. габариты Земли намного превосходят их. При определении расстояния между планетой и поверхностным телом рассматривается только радиус Земли, т.к. высота расположения тела пренебрежимо мала в сравнении с ним. Получается, что Земля притягивает тело с силой F=M/R², где M – масса Земли, R – ее радиус.
Согласно закону всемирного тяготения, ускорение тел при действии силы тяжести на поверхности Земли равно: g=G•M/ R². Здесь G – гравитационная постоянная, численно равная примерно 6,6742•10^(−11).
Ускорение свободного падения g и радиус земли R находятся из непосредственных измерений. Константа G с большой точностью определена в опытах Кэвендиша и Йолли. Итак, масса Земли M=5,976•10^27 г ≈ 6•10^27 г.
Все тела, обладающие массой, возбуждают в окружающем пространстве гравитационные поля, подобно тому, как электрически заряженные частицы образуют вокруг себя электростатическое поле. Можно предположить, что тела несут в себе гравитационный заряд, аналогичный электрическому, или, по-другому, обладают гравитационной массой. С высокой точностью было установлено, что инертная и гравитационная массы совпадают.
Пусть имеется два точечных тела массами m1 и m2. Они удалены друг от друга на расстояние r. Тогда сила гравитационного притяжения между ними равна: F=C·m1·m2/r², где С – коэффициент, который зависит лишь от выбранных единиц измерения.
Если на поверхности Земли имеется небольшое тело, его размерами и массой можно пренебречь, т.к. габариты Земли намного превосходят их. При определении расстояния между планетой и поверхностным телом рассматривается только радиус Земли, т.к. высота расположения тела пренебрежимо мала в сравнении с ним. Получается, что Земля притягивает тело с силой F=M/R², где M – масса Земли, R – ее радиус.
Согласно закону всемирного тяготения, ускорение тел при действии силы тяжести на поверхности Земли равно: g=G•M/ R². Здесь G – гравитационная постоянная, численно равная примерно 6,6742•10^(−11).
Ускорение свободного падения g и радиус земли R находятся из непосредственных измерений. Константа G с большой точностью определена в опытах Кэвендиша и Йолли. Итак, масса Земли M=5,976•10^27 г ≈ 6•10^27 г.